第三十五條
受剪截面
一、各截面的剪力設計值VSd應滿足下列條件：
VSd£ Vpl.Rd
式中： Vpl.Rd = Av (fy /
) / gM0
二、抗剪面積Av 可按表十六採用。
|
表十六 抗剪面積 |
|
截面形式 |
Av |
|
a. 荷載平行於腹板的熱軋Ｉ型鋼、H型鋼及槽鋼 |
1.04 h tw |
|
b. 荷載平行於腹板的焊接Ｉ形鋼、H型鋼、槽鋼及箱型鋼 |
S (d tw) |
|
c. 荷載平行於翼板的焊接Ｉ形鋼、H型鋼、槽鋼及箱型鋼 |
A - S (d tw) |
|
d. 荷載平行於深度的熱軋矩形鋼管 |
A h / (b + h) |
|
e. 荷載平行於寬度的熱軋矩形鋼管 |
A b / (b + h) |
|
f. 圓形鋼管及均厚管道 |
2 A / p |
三、其他截面形式Av可以按類似的方法計算。
四、除Av.net ³ (fy / fu) Av外，抗剪的驗算不允許有螺栓孔。當Av.net少於以上的數值，Av.net可取有效抗剪面積(fy / fu) Av.net。
五、此外，當下列情況發生時，剪力挫曲承載力亦應按第四十條所述的方法驗算：
－非加勁腹板
－加勁腹板
式中 kt = 挫曲係數 (見表二十一)
六、構件端部的塊狀剪力撕裂準則應按第五十條進行驗證。
第三十六條
同時受彎、受剪及受軸力之截面
一、第一、二級截面應滿足下列條件：
(一) 軸力：
(見第三十二條或第三十三條)
(二) 剪力：
(見第三十五條)
(三) 彎矩：
(見表十七)
式中：MN.V.Rd＝同時受軸力及剪力下塑性彎矩的折減承載力
(四) 複合彎矩
二、第三級截面應滿足下列條件：
(一) 軸力：
(見第三十二條或第三十三條)
(二) 剪力：
(見第三十五條)
(三) 彎矩：
(見第三十四條)
(四) 相互公式：
當
當
式中：r = (2 VSd / Vpl.Rd – 1)2
三、此外，構材的挫曲或側向扭轉挫曲亦應進行驗算(見第三節)。
表十七 同時受軸力及剪力下塑性彎矩承載力的折減 (第一級或第二級) |
|||
|
截面形式 |
軸力水平 |
剪力水平 |
|
|
|
|
||
|
|
低 |
|
|
|
高 |
|
|
|
|
|
低 |
|
|
|
高 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
低 |
|
|
|
高 |
|
|
|
|
|
低 |
|
|
|
高 |
|
|
|
|
|
低 |
|
|
|
高 |
|
|
|
|
表中：
低軸力：
高軸力： |
|||
構件抗力
第三十七條
受壓構件的挫曲承載力
一、受壓構件的挫曲承載力設計值應滿足下列條件：
NSd£ Nb.Rd
式中 Nb.Rd = cbA A fy / gM1
bA = 1 適用於第一、二、三級截面
bA = Aeff / A 適用於第四級截面
c = 相關挫曲狀態下的折減係數
二、均勻截面的c值可按下列公式計算：
式中
a = 缺陷係數 (見表十八)
三、幾何細長比
按下式計算：
式中
(fy－N/mm2)
= 細長比
四、細長比
應按下式計算：
式中 
= 受壓構件雙端受側向固定的挫曲有效長度，可保守地取其相等於構件的長度。
i = 參考軸的回轉半徑，應按毛截面特性計算。
五、非均勻構件截面變化的c值，可按二階分析方法驗證。
|
表十八 截面挫曲曲線的選擇 |
||||
|
截面形式 |
限制 |
挫曲 方向 |
挫曲 曲線 |
缺陷 係數a |
軋制Ｉ形截面 |
h / b > 1.2 及tf £ 40 mm |
對y軸 對z軸 |
a b |
0.21 0.34 |
|
h / b > 1.2 及 40 < tf < 100 |
對y軸 對z軸 |
b c |
0.34 0.49 |
|
|
h / b £ 1.2 及 tf £ 100 mm |
對y軸 對z軸 |
b c |
0.34 0.49 |
|
|
h / b £ 1.2 及 tf > 100 mm |
對y軸 對z軸 |
d d |
0.76 0.76 |
|
|
焊接Ｉ形截面 |
tf £ 40 |
對y軸 對z軸 |
b c |
0.34 0.49 |
|
tf > 40 |
對y軸 對z軸 |
c d |
0.49 0.76 |
|
|
空心截面 |
熱軋 |
對任意軸 |
a |
0.21 |
|
焊接箱形截面 |
一般 |
對任意軸 |
b |
0.34 |
U形、 L形、 T形及實心截面 |
對任意軸 |
c |
0.49 |
|
|
註：表中所列之挫曲曲線可作參考引用，更詳細之數據資料可參閱ENV1993-1-1。 |
||||
第三十八條
同時受彎及受壓之挫曲承載力
一、第一、二級截面的構件同時受彎及受壓下應滿足下列條件：
式中：
= 取
，
中較少的值
,
,
,
= 應按第三十七條計算
,
= 受彎挫曲的等效彎矩係數（見表十九及第四款)
二、若側向扭轉挫曲是一種潛在破壞模式亦應滿足下列條件：
式中：
= 應按第三十九條計算
側向挫曲的等效彎矩係數（見表十九及第四款)
三、屬第三、四級截面之構件，其驗證應符合ENV1993-1-1第5.5.4章的要求。
四、等效彎矩係數
,
,
可根據兩點支撐之間的彎矩圖形從表十九中獲得：
係數 彎矩軸 支承方向
y – y z – z
z – z y – y
y – y y – y
|
表十九
等效彎矩係數 |
|
彎矩圖 |
等效彎矩係數 |
|
a). 端部彎矩
|
|
|
b). 受側向荷載的彎矩
|
|
|
c). 受側向荷載的彎矩
|
|
第三十九條
梁的側向扭轉挫曲承載力
一、有充分側向支撐的梁不需進行側向挫曲承載力之驗算。
二、無充分側向支撐的梁之挫曲彎矩承載力設計值應滿足下列條件：
MSd£ Mb.Rd
式中：
= 1 適用於第一、二級截面
適用於第三級截面
適用於第四級截面
= 側向挫曲折減係數
三、cLT可按下式計算：
式中：
軋制截面(曲線a)
焊接截面(曲線c)
四、幾何細長比
按下式計算：
式中：
(fy：N/mm2) (見第三十七條)
It = 扭力常數
Iw = 翹曲常數
C1 = 受荷載及支承狀態影響的係數，可由y及k確定（見表二十)
y = 側向支撐間的端部彎矩比
k = 在平面上端部轉動的有效長度係數，當端部完全固定時等於0.5，無固定轉動時等於1.0，一端固定另一端無固定時等於0.7
五、若
，側向挫曲不需要考慮。
|
表二十 對應k值之C1係數：端部彎矩荷載 |
|||
|
荷載及支承狀態 |
彎矩圖 |
k值 |
C1 值 |
|
|
y = +1
|
1.0 |
1.000 |
|
0.7 |
1.000 |
||
|
0.5 |
1.000 |
||
|
y = 0
|
1.0 |
1.879 |
|
|
0.7 |
2.092 |
||
|
0.5 |
2.150 |
||
|
y = -1
|
1.0 |
2.752 |
|
|
0.7 |
3.063 |
||
|
0.5 |
3.149 |
||
|
|
|
1.0 |
1.132 |
|
0.5 |
0.972 |
||
|
|
|
1.0 |
1.285 |
|
0.5 |
0.712 |
||
第四十條
腹板的剪力挫曲承載力
一、設計基本要求
(一) 當非加勁腹板的d/tw值大於69e加勁腹板的d/tw大於
(kt值見表二十一)，應對其剪力挫曲承載力進行驗算；
(二) 當腹板無中間橫向加勁板或只有加勁板在支承點時，剪力挫曲承載力可按以下方法計算：
§ 後挫曲方法－在本條後面部份詳述
§ 張力區方法－應按ENV1993-1-1第5.6條款所述方法計算
二、後挫曲方法
(一) 使用後挫曲方法的剪力挫曲承載力設計值Vba.Rd應符合下列條件：
式中：
為受腹板細長度lw影響的後剪力挫曲強度(見表二十二)
(二) 腹板細長比應按下式計算：
式中： kt = 挫曲係數(見表二十一)
|
表二十一 挫曲係數kt |
|
|
腹板在支承點有橫向加勁板及 |
kt |
|
無中間橫向加勁板 |
5.34 |
|
a / d < 1 Œ之中間橫向加勁板 |
4 + 5.34 / ( a / d)2 |
|
a / d ³ 1 Œ之中間橫向加勁板 |
5.34 + 4 / (a / d)2 |
|
註： Œ a = 橫向加勁板的間距 d = 腹板深度 |
|
|
表二十二 剪力挫曲強度 |
|||
|
|
|
|
|
|
|
|
|
|
|
註： fyw = 腹板的屈服強度 |
|||
三、同時受彎及受剪
(一) 只要VSd不超過Vba.Rd的一半，同時受剪的截面彎矩承載力設計值不需要折減；
(二) 當VSd超過Vba.Rd的一半，截面的彎矩承載力設計值應按下列公式折減：
式中：
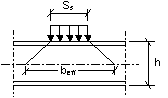
Mf.Rd = 淨翼板上的塑性彎矩承載力設計值，考慮受壓翼板的有效寬度beff
第四十一條
翼板之挫曲
要避免受壓翼板的挫曲，腹板的d/tw比值應符合下列條件：
式中：
Aw＝腹板面積
Afc＝受壓翼板面積
fyf＝受壓翼板的屈服強度
k ＝0.3適用於一級截面之翼板
0.4適用於二級截面之翼板
0.55適用於三級或四級截面之翼板
第四十二條
腹板受外力作用之承載力
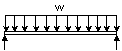
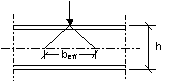
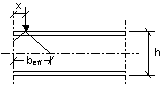
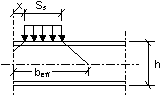
一、非加勁腹板透過翼板承受外力作用之承載力主要受制於下列其中一種破壞模式(圖二)。
(一) 靠近翼板的腹板產生壓碎，翼板並同時出現塑性變形；
(二) 腹板以局部挫曲的形式出現皺曲，靠近翼板的腹板產生壓碎，翼板並同時出現塑性變形；
(三) 構材大部份的深度產生腹板挫曲。
|
|
|
|
|
圖二 腹板受外力作用下的破壞模式 |
||
二、當外力透過翼板一端再由腹板抵抗剪力，腹板受外力作用之承載力應取以下較少的情況：
§腹板壓碎承載力 Ry.Rd (見第四款)
§腹板皺曲承載力 Ra.Rd (見第五款)
三、當外力透過翼板一端，再直接由腹板傳到另一端翼板，腹板受外力作用之承載力應取以下較少的情況：
§腹板壓碎承載力 Ry.Rd (見第四款)
§腹板挫曲承載力 Rb.Rd (見第六款)
四、腹板壓碎承載力 Ry.Rd
Ｉ形、Ｈ形或Ｕ形截面的腹板壓碎承載力設計值應按下式計算：
式中：
ss = 支承長度
但bf不應超過25tf及在構材端部sy須減半。
sf.Ed = 翼板的縱向應力
五、腹板皺曲承載力Ra.Rd
Ｉ形、Ｈ形或Ｕ形截面的腹板皺曲承載力設計值應按下式計算：
但ss/d不應超過0.2，當構件亦同時承受彎矩，應同時滿足下列條件：
六、腹板挫曲承載力Rb.Rd
Ｉ形、Ｈ形或Ｕ形截面的腹板挫曲承載力設計值應
將腹板考慮成虛擬之受壓構件，並用下式計算有效寬度beff：
(見表二十三)
腹板挫曲承載力應按第三十七條的方法，採用c類曲線及bA等於1。
|
表二十三 計算腹板側向挫曲的有效寬度 |
|
|
|
|
|
|
|
|
|
|
|
|
|
